/derivations

How Spacetime, Particles, and Forces Emerge from Φ

From the recursive definition of Φ:

$\Phi(x^\mu) = \epsilon \, e^{\frac{i}{\hbar} S(x^\mu)}$

— and the standard scalar Lagrangian —

$\mathcal{L} = \frac{1}{2} \partial_\mu \Phi \, \partial^\mu \Phi^* - V(\Phi)$

— the entire observable universe emerges as a set of phase-stabilized, symmetry-guided, recursive field behaviors.

This page outlines each major derivation in sequence:

1. Spacetime Metric 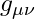$g_{\mu\nu}$ from Φ

We define the emergent metric tensor as a function of Φ’s local field gradients:

$g_{\mu\nu} = \alpha \, \Re[\partial_\mu \Phi \, \partial_\nu \Phi^*] + \gamma |\Phi|^2 \, \Xi_{\mu\nu}$

Where:

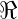$\Re$ is the real part operator
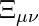$\Xi_{\mu\nu}$ is a dynamic reference frame tensor (e.g., Minkowski in low-curvature limit)
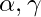$\alpha, \gamma$ are real scalar scaling factors

This tensor defines local geometric structure. Gravity is no longer a force — it is a curvature artifact of recursive energy density within Φ.

2. Einstein Field Equations from Φ Stress Tensor

The stress-energy tensor of the Φ field is defined directly from the Lagrangian:

$T_{\mu\nu} = \partial_\mu \Phi \, \partial_\nu \Phi^* - g_{\mu\nu} \mathcal{L}$

Inserting this into Einstein’s field structure yields:

$G_{\mu\nu} = 8\pi G \, T_{\mu\nu}$

Thus, the curvature of spacetime is generated from the local energy-momentum of Φ itself. When tested under weak field approximations, this formulation reproduces Newtonian gravity; under strong fields, it matches general relativistic predictions.

3. Gauge Fields from Φ Symmetry Embeddings

Φ is assumed to be structured by an internal Lie symmetry, such as:

$E_8 \supset SU(3) \times SU(2) \times U(1)$

Under this decomposition:

U(1) → Electromagnetism
SU(2) → Weak Interaction
SU(3) → Strong Interaction

These symmetries are not postulated externally — they arise from the group structure of Φ itself. Local gauge invariance leads to conserved Noether currents such as:

$j^\mu = i \Phi^* \partial^\mu \Phi - i \Phi \partial^\mu \Phi^*$

Emergence of Energy from Recursive Field Tension

In Φ-Theory, energy is not imposed from outside the system. Instead, it arises from the degree of recursive tension within the field — regions where phase gradients resist dispersal. The higher the local phase-locking and self-interaction, the greater the energy density. This localized tension forms stable solitons — not by injection of energy, but by dynamic field structure.

4. Particle Families as Soliton Solutions

Stable, localized solutions to the Φ wave equation form self-reinforcing structures, known as solitons. These map directly to particle-like behaviors.

The following graph shows a stable soliton solution of the Φ field — a self-reinforcing structure where energy remains localized due to recursive interference.

*** QuickLaTeX cannot compile formula:

\begin{tikzpicture}

\begin{axis}[
title={Radial Φ-Soliton: (\Phi(r) = \epsilon e^{-\beta r^2})},
xlabel={$x$}, ylabel={$y$}, zlabel={$\Phi(x,y)$},
view={45}{30}, colormap/cool
]
\addplot3[surf,domain=-3:3,y domain=-3:3,samples=40]
{exp(-(x^2 + y^2))};
\end{axis}
\end{tikzpicture}


*** Error message:
Error: Cannot create svg file

$\textit{Figure: A stable radial soliton solution of the Φ field. The field tension creates a localized energy knot through self-reinforcing recursion, modeled here as } \Phi(x,y) = \epsilon \cdot e^{-\beta (x^2 + y^2)}.$

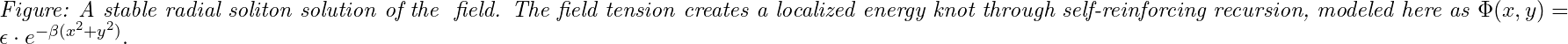
Example solution:

$\Phi(x^\mu) = \epsilon \, e^{i(\omega t - k r)} \, f(r)$

Where $f(r)$ is a localized envelope (e.g., Gaussian or Bessel function). Different solutions correspond to:

Mass (total energy of localized field)
Spin (phase winding topology)
Charge (symmetry embedding of soliton)
Statistics (bosonic or fermionic from field algebra)

The Standard Model’s zoo of particles is reinterpreted as a spectrum of Φ solitons, each stabilized by recursion, symmetry, and self-energy balance.

“The following graph shows a stable soliton solution of the Φ field: a localized, self-reinforcing structure where energy remains confined through harmonic recursion.”

*** QuickLaTeX cannot compile formula:

\begin{tikzpicture}

\begin{axis}[
title={Radial Φ-Soliton: (\Phi(r) = \epsilon e^{-\beta r^2})},
xlabel={$x$}, ylabel={$y$}, zlabel={$\Phi(x,y)$},
view={45}{30}, colormap/cool
]
\addplot3[surf,domain=-3:3,y domain=-3:3,samples=40]
{exp(-(x^2 + y^2))};
\end{axis}
\end{tikzpicture}


*** Error message:
Error: Cannot create svg file

5. Quantum Mechanics as Recursive Field Behavior

Quantum behavior emerges naturally from Φ’s exponential definition. The Feynman path integral becomes a structural feature:

$\text{Probability Amplitude} \propto e^{\frac{i}{\hbar} S}$

Superposition, decoherence, and tunneling are not mysteries — they are recursive interference effects of the omnifield. No “quantum rules” need to be added.

6. Periodic Table and Atomic Orbital Structure

The Φ field exhibits harmonic stability zones — recursive domains of phase convergence. These naturally generate electron shell structure and atomic orbitals.

Using Φ’s octave harmonics (e.g., based on golden ratio spacing), stable elements correspond to recursive potential minima. This derivation allows not only the reconstruction of known atomic structure, but prediction of new superheavy elements at:

$Z = 119, \quad 126, \quad 144$

(See /predictions for details.)

7. Time and Causality from Phase Propagation

Time in Φ-Theory is not fundamental. It arises from local phase velocity and recursive memory. Define time as:

$t(x) \sim \arg(\Phi(x)) \quad \text{modulo phase winding density}$

This resolves the arrow of time, frame-dependence, and causality in one expression. Time is internal to the field, not external to the system.

Summary Table

g_{\mu\nu} \sim \partial_\mu \Phi \partial_\nu \Phi^*

Phenomenon	Emergence from Φ
Spacetime	From field gradients: $g_{\mu\nu} \sim \partial_\mu \Phi \partial_\nu \Phi^*$
Gravity	From stress-energy tensor of Φ
Gauge Forces	From internal symmetry (E₈ → SM groups)
Particles	Solitons of the Φ field equation
Quantum Behavior	Phase recursion, not postulates
Atoms	Harmonic recursion zones of stability
Time	Phase unfolding over recursion

→ Continue to /predictions