/axiom

The Foundational Postulate of Φ-Theory

Definition

Φ-Theory is built on a single postulate:

All physical phenomena — including spacetime, energy, particles, fields, and information — emerge from the behavior of a single complex scalar field Φ defined over spacetime.

There are no additional fields, forces, particles, or assumptions. Φ is the only primitive. Its behavior is recursive and determined by a local action function $S(x^\mu)$ , leading to the core definition:

$\Phi(x^\mu) = \epsilon \, e^{\frac{i}{\hbar} S(x^\mu)}$

Where:

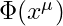$\Phi(x^\mu)$ is a complex scalar field over spacetime coordinates $x^\mu$
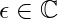$\epsilon \in \mathbb{C}$ is a normalization amplitude
$S(x^\mu)$ is the local action, integrated from a standard Lagrangian
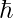$\hbar$ is Planck’s reduced constant

Ontological Position

Φ is not embedded in spacetime. Φ generates spacetime. Its local gradients define curvature. Its recursive evolution defines causal flow.

There is no a priori space, time, or energy. These emerge as second-order properties from field recursion. Observable entities (particles, charges, masses) are structured solitons within Φ.

The theory assumes:

1 field: Φ
1 law: recursion via action phase
0 free parameters (outside $\epsilon$ , which normalizes the solution domain)

Why This Axiom?

This postulate was chosen not because it is intuitive, but because it is sufficient.

All of physics may be rewritten from this one equation, assuming:

Spacetime geometry is emergent from field gradients
Mass and charge are emergent from topological solitons
Quantum mechanics emerges from recursive interference
Field symmetry defines all interaction families

This eliminates the need for postulating particles, dark matter, dark energy, or inflation — they are to be derived from field dynamics or rejected.

Scope of Application

This postulate, if valid, applies to:

General Relativity (recovered from stress-energy in Φ)
Standard Model (reconstructed via symmetry embeddings in Φ)
Quantum Mechanics (arising from phase recursion)
Cosmology (expansion, curvature, entropy gradients derived from Φ-scale dynamics)
Atomic structure and chemistry (modeled as stable Φ solitons)
Consciousness and life (self-reflective Φ loops, not added to matter)

Φ is not one force among many — it is the background field from which all other appearances emerge.

Final Statement

The Omnifield Axiom posits the irreducibility of physical law. If any field other than Φ is required to explain reality, the theory is invalid.

This page defines Φ. The next pages define how everything else — geometry, motion, matter, and observation — follows from it.

→ Continue to /formula