/formula

The Mathematical Heart of the Omnifield Axiom

The Core Expression

Φ-Theory is rooted in a single, recursive field definition that governs the emergence of all phenomena:

$\Phi(x^\mu) = \epsilon \, e^{\frac{i}{\hbar} S(x^\mu)}$

This is not a symbolic shortcut. It is the fundamental operation of the universe.

Each component is defined as:

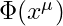$\Phi(x^\mu)$ : A complex scalar field over four-dimensional spacetime
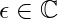$\epsilon \in \mathbb{C}$ : A field-normalizing amplitude (context-dependent)
$S(x^\mu)$ : The local action, a functional of the field configuration
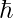$\hbar$ : The reduced Planck constant, scaling phase contributions

Action and Lagrangian Definition

The action is computed from a standard complex scalar field Lagrangian:

$\mathcal{L} = \frac{1}{2} \partial_\mu \Phi \, \partial^\mu \Phi^* - V(\Phi)$

$S(x^\mu) = \int \mathcal{L} \, d^4x$

The potential $V(\Phi)$ may take quadratic or quartic forms (e.g., $m^2 |\Phi|^2 + \lambda |\Phi|^4$ ) depending on symmetry-breaking conditions or soliton stability.

Field Equation of Motion

Applying the Euler-Lagrange equation yields the standard scalar field wave equation:

$\Box \Phi + \frac{\partial V}{\partial \Phi^*} = 0$

$\text{with } \Box \equiv \partial^\mu \partial_\mu$

This governs how Φ propagates, interacts, and self-organizes. When nonlinear potentials or boundary conditions are introduced, this equation admits localized, self-stabilizing solutions — solitons — which appear as particles.

Recursive Phase Behavior and Quantum Dynamics

Because the field is defined recursively through an exponential of the action, its structure encodes the same weighting as the Feynman path integral:

$\text{Probability} \propto e^{\frac{i}{\hbar} S}$

Quantum mechanical superposition and interference are not added onto Φ. They are inherent to its phase structure. All quantum behavior — entanglement, tunneling, measurement collapse — arises from Φ’s recursion dynamics, not from postulated rules.

Why This Formula?

This is not a derived equation. It is a postulate. Its structure was selected for three reasons:

It yields known physical behaviors (GR, QM, gauge fields) under known limits
It contains no arbitrary additions or external constructs
It is testable, falsifiable, and structurally minimal

From this equation, we do not just describe reality. We generate it.

→ Continue to /derivations